わたしのカメラ三昧 第10回 蛇腹を作る （その１） 蛇腹方程式
蛇腹を作る （その１） 蛇腹方程式
この連載の第7回でBaby Suzukaという蛇腹カメラを紹介した。そのカメラは手に入れたとき蛇腹に大きな穴があいていて，それを塞いだのであるが，詳細に見ると他にもいくつかのピンホールがあった。それらを和紙で塞いだが，塞げば破れ，また塞げばまた破れるといったもぐら叩きが続いた。
そこで抜本的な治療法としては蛇腹の取替えしかないと思い，蛇腹を自作することにした。
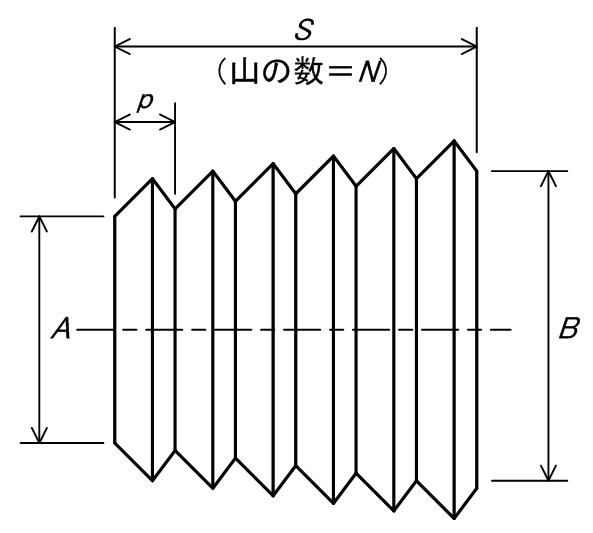
まず，蛇腹であるが，たとえばその側面は図１のようになっている。
図１．蛇腹の側面図（概念図）
Baby Suzukaの蛇腹の寸法を測ると，山・谷ともに5mm程度であった。亀吉は素人だから取り敢えず和紙のような丈夫な紙で四角錐台の筒を作って，5mmごとに山・谷・山・谷・・・というふうに折り曲げればよいだろう程度に考えた。
ところが，何か参考になることはないかと思ってインターネットで検索したところ，そんな単純な考えでは駄目なことがわかった。一番重要な点は，山と谷の斜面の寸法である。当然であるが「折り畳める」という条件が課せられているということを認識したのである。図２をご覧いただきたい。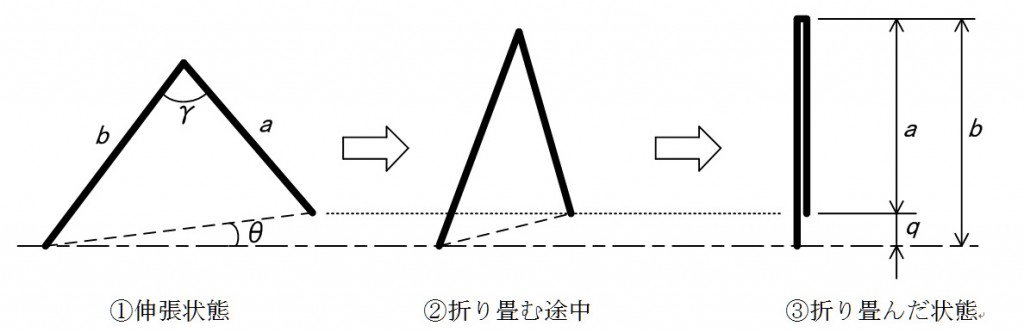
図２．蛇腹を折り畳む過程（一山を示す）
図２の①は蛇腹を伸張したときの一山を側面から見た図である。これを折り畳むとすると，その途中で②の状態があり，最終的に③のようになる。このとき山の両斜面の垂直方向の高さの差（図2のq）が一定であることが必要なのである。とにかく，③の状態になることが不可欠である。このことを理解した。
では，その条件のもとで，山の両斜面の長さはどのように決定できるのであろうか？また，それに基づいた蛇腹の展開図はどのようになるのだろうか？すなわち，ここでの最終目標は図３に示す展開図を作図するために必要な各寸法を理論的に決定する方法を確立することである。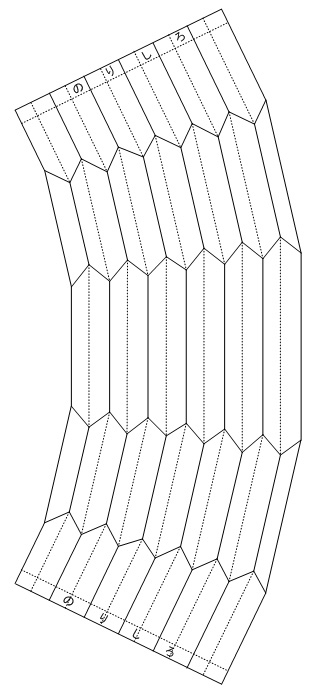
図3．蛇腹の展開図の一例
図3において，点線は谷折り，実線は山折りを示す。（ただし，輪郭およびのりしろ部分を除く。）この点線と実線の間隔を求めるのが今回の最重要目標である。
以下，亀吉が独断で検討した結果をご紹介しよう。間違いがあるかも知れないし，まだすっきりしない点もある。この点はあらかじめご承知置き願いたい。
１．山の両斜面の寸法
1.1 基本式
蛇腹の一山に注目する。
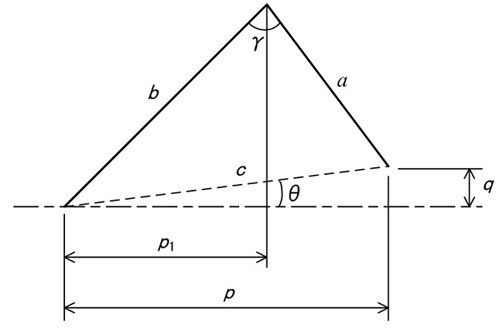
図4を参照されたい。その頂点の角度をγとし，頂点から両谷底までの（斜面の）長さをaおよびbとする。また，両谷底間を直線で結んだ長さをcとし（以下，底辺と呼ぶ），その直線の水平方向に対する角度をθとする。さらに，両谷底間の水平距離をp とし，両谷底の高さ（深さ？）の差をqとする。
蛇腹一山の3辺a,b,cおよび頂点の角度γに関してつぎの式が成り立つ。（余弦定理）
また，その三角形の下の直角三角形に対しては三平方の定理（ピタゴラスの定理）から
である。さらに，蛇腹がきちんと折り畳めるためには最初に述べたように
という条件が必要である。
以上の3つの式が出発点となる。
図4．蛇腹を伸張したときの一山
1.2 斜面aの計算
まず，式(1)および(2)からcを消去する。
つぎに，式(4)に式(3)の関係を代入すると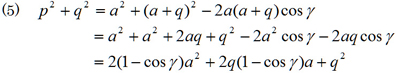
となる。整理すると、
となるが，この式はaについての二次方程式である。根（解）の公式を適用して解く。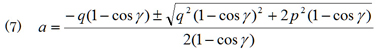
ところで， a＞0でなければならないから，採用できる解は
に限られる。
式(8)を眺めると，1-cos γがやたら目につく。分子，分母を1-cos γで除してやると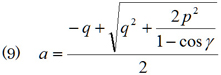
を得る。このままでもいいのだが，公式
を適用すると，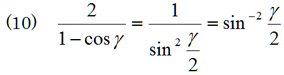
であるから，式(9)は
と書き表すことができる。
であるので，cosecを使って書き表すこともできるが，cosecはあまり一般的でないのでやめておく。
一応上の式でを求めることができるのであるが，蛇腹を伸張したときの傾斜角θを使って書き表すことを考える。
を式(11)に代入すると、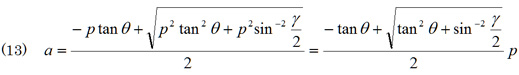
となる。この式でp=1とした場合のaをan として
である。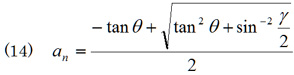
を基準化式と呼んでおこう。すなわち、
である。
1.3斜面bの計算
さて、bについては式(3)にaを代入すればよい。式(11)を用いると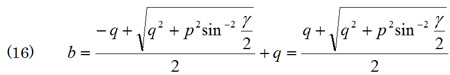
となる。さらに式(12)の関係を適用すると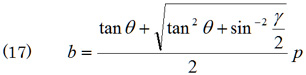
を得る。基準化式は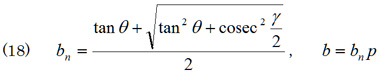
として与えられる。aとb（あるいはanとbn）は非常にすっきりとした対称的な式となった。
２．展開図の寸法
2.1 台形の高さの計算
蛇腹を作る際，図3のような展開図が必要になる。その各面は台形である。（特殊な場合は長方形，あるいはさらに特殊な場合には正方形ということもありうる。）その台形の高さＬはつぎの式で計算できることは容易に理解できるであろう。（図6参照。）
ここで，Ｎは山（あるいは谷）の数である。一般にはＮは正の整数であるが，0.5だけの端数の付くことがある。これは山（または谷）から始まって谷（または山）で完結するような場合である。もっとも，0.5というのは概数であって，正確な小数は山の寸法がわからなければ決まらない。（図4を例にとれば，P1 / Pまたは1-P1 / Pである。）山の寸法を決めるためにはpの値が必要になるが，そのためにはNが必要になる（∵p = S /N）。
かくして，堂々巡りになる。どうしても正確な値が必要なら繰り返し計算して収束値を求めることになろう。（ここではこれ以上立ち入らない。）
参考までにp1を求める式を誘導しておこう。
図4から明らかなように，
である。θは分かっているが，αが分かっていない。αを求めよう。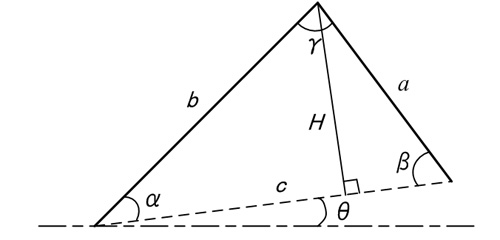
図5．角度αとβを求める作図
蛇腹の一山の頂点から底辺cへの垂線の長さをHとすると，（図5参照。）
である。ここで，a+b+γ=πであるから
である。この関係を式(20)に代入して加法定理を適用すると、
となる。両辺をcos αで割ると
となるから，これをtan αについて解くと、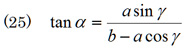
を得る。すなわち，角度αは
として計算できる。
ついでに角度βも計算しておこう。式(22)に式(26)を代入すると
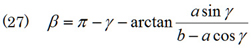
となるが，αを求めたのと同じ手順を踏んで，（計算過程は省略）
を得る。やはり式(26)と対称な式となった。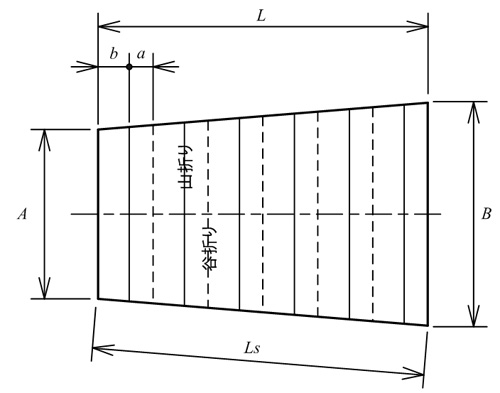
図6．蛇腹の一側面の展開図（N=6の場合）
2.2 台形の上底と下底の決定
台形の上底と下底（図6のAとB）の寸法はカメラの寸法に関わる事柄であり，特に計算するほどのことはないと考えていた。また，2つの台形面が接する稜線での折り曲げは両台形面に等分に配分されるものと考えていた。つまり，図7の①のように考えていたのである。
ところが，ここまで述べてきた「蛇腹方程式」によって試算した結果で描いた展開図は図7の②のようになったのである。寸法誤差や例題の特殊性のためではないかと疑って異なる条件でも描いてみたが，結果は同じであった。
つまり，蛇腹のつづら折れは隣り合う両面に対して等分に配分されないのである。のみならず，図7の②からわかるように「山から始まる面は侵食されず，谷から始まる面のみが侵食される」のである。侵食などどうも言葉がよくないのだが，正式な呼び名がわからないので仕方がない。しかし，亀吉が言いたいことはお分かりいただけると思う。
要するに台形の上底と下底は以上のことを踏まえて決定するということになる。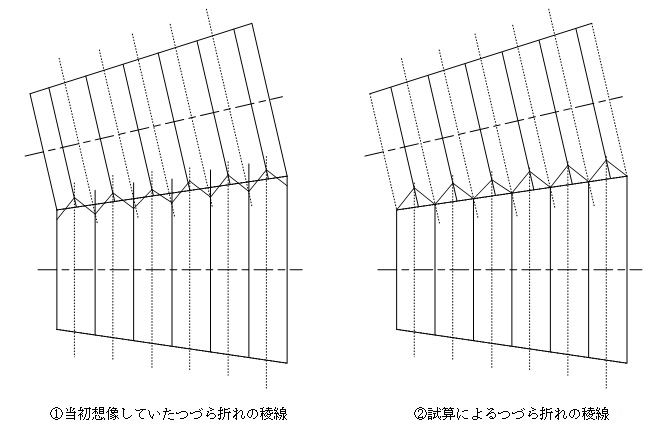
図7蛇腹の隣り合う稜線でのつづら折れ
2.3 台形の斜辺の計算
台形の斜辺，すなわち図6のLsは作図自体には不要である。つまり，高さおよび上底と下底が決定すれば台形は確定する。それでもあえて斜辺の計算を持ち出したのは，隣り合う台形の整合性を検証するがためである。隣り合う台形の斜辺の寸法が異なれば展開図は描けない。
その斜辺の計算は簡単である。図6から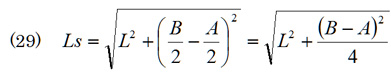
である。
３．補足事項
以上，蛇腹の寸法決定のための基礎的な理論について考えてきた。しかし，実際の蛇腹作りに適用するにはつぎのような制約あるいは前提が課せられる。
（１）蛇腹収納時の厚み
（２）蛇腹の最大外形寸法
（３）蛇腹の山の頂点の角度
上記はいずれも相互に関連しているのでトレードオフが必要な場合もあろう。
では，個別について簡単に考えてみよう。
まず，蛇腹収納時の厚みの制約である。これは蛇腹の素材（塗装などの厚みを含む）の厚みをTとし，蛇腹の山の数をNとすると，2NTが蛇腹を畳んで収納する空間の深さ未満でなければならないということである。したがって，むやみに山の数を多くしたり，素材の厚みを増したりしてはいけない。
つぎに，蛇腹の最大外形寸法については，収納時他の部品などとの干渉が問題となることがあるのである。蛇腹収納場所にねじやばねなどがあって，これらが蛇腹と接触することによって蛇腹を傷めることが考えられる。
最後に蛇腹の山の頂点の角度の問題。手許にあるいくつかの蛇腹カメラを伸張した状態で観察すると，殆どの蛇腹はその山の頂点が90度に近い角度のようである。一方，インターネットで検索したところによると，蛇腹の頂点の角度は70度前後が最適だとのことである。ただし，これはカメラの蛇腹でない。しかし，蛇腹の一般的性質・制約として捉えると，蛇腹の頂点の角度は60度から90度の間であることが望ましいようである。特に，90度を超えると蛇腹の素材に対する力学的な負担が大きくなるのでやめたほうが良かろうとは直感的にも頷ける。
４．終わりに
蛇腹方程式という呼称は亀吉が勝手に唱えているだけである。一般に通ずる用語かどうかは定かでないことをお断りしておく。
(次号に続く)
■2012年4月11日 木下亀吉
｢わたしのカメラ三昧｣に掲載されているすべての画像・文章は作者の木下亀吉様が所有しています、許可無く無断で複製・配布することはご遠慮下さい。
