わたしのカメラ三昧 第11回 蛇腹を作る (その2) 蛇腹の設計
蛇腹を作る (その2) 蛇腹の設計
蛇腹方程式を提示したので(4月11日掲載),つぎは蛇腹の設計・製作となるはずである。
しかし,どうも力が入らない。その理由は2つある。
① 蛇腹の設計において,いま一つ解けない問題がある。
② 修復の対象にしていたカメラ(Baby Suzuka II)のシャッターの調子が悪く,蛇腹を新調してもカメラとしての機能が充分果たせない。つまり,自作蛇腹の検証ができない。 上記①は何とかごまかすことができそうだが,②はごまかしようがない。蛇腹の破れたカメラをインターネットやリサイクルショップで探してきたが,見つからない。どうしよう,どうしようと悩んでいるうちに時間が経過してしまった。
このまま悩んでいてもしようがないので①はごまかすとして,②はシャッターの不調が目立たない状況での撮影に制限することにした。あるいは最悪の場合試写検証なしの記事にしよう。
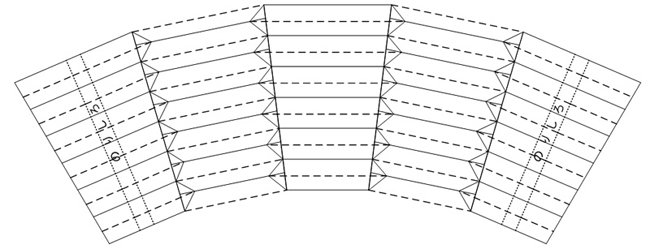
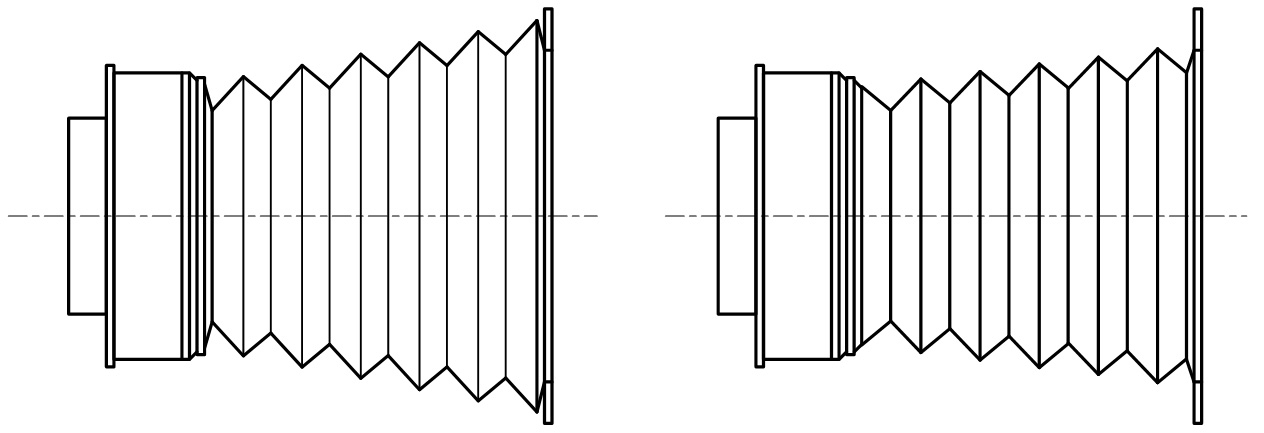
まず,ベビースズカの蛇腹の原状をスケッチした。それを図1に示す。
図1で,左の図は蛇腹の側面であり,右の図は上から(または下から)見た図(以下,平面図と呼ぶ)である。おわかりのようにカメラ本体側の幅が異なっている。それはベビースズカの場合,画面の寸法が縦40 mm,横30 mmの長方形であるからである。もちろん,レンズは円形であるのでレンズ側の寸法は等しい。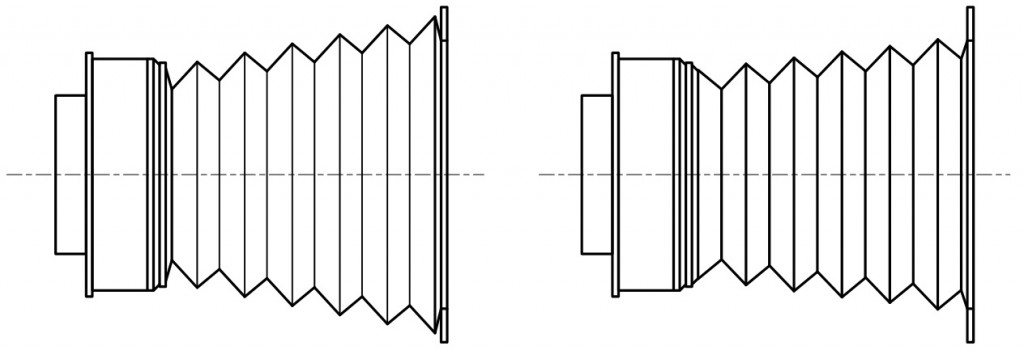
図1.ベビースズカの蛇腹の原状(左は側面図,右は平面図)
ここで一つ気になるのは山(または谷)から始まって谷(または山)で終っている点である。つまり,前回述べたところの山の数Nが整数ではないのである。なぜこうなのか?一般的にカメラの蛇腹というのはこうなのか?とにかく,亀吉の理論ではNが整数でないとやりにくいのである。
そこで,原状にはこだわらず,N=6として設計することにした。1/2山だけ多くなるが,特に問題はないであろう。(ただし,折り畳んだとき蛇腹の素材1枚分の厚みが増すことに注意が必要。)
蛇腹を伸張したときの大まかな寸法は①レンズ取り付け穴,②カメラ本体側の切り抜き,および③長さの3つが分かれば確定する。
まず①であるが,ベビースズカの蛇腹部分を分解したらレンズ部分との結合部に図2の左に示すような座金が出てきた。蛇腹の一方でこの座金を包み込み,レンズを囲む筒を直径22.3 mmの穴に通してナットで固定するのである。だから,蛇腹のレンズ側の一辺は33 mm,余裕を見て34 mmほどと見積もることができる。
つぎに②は図2の右のようであった。この長方形の切り抜きの中に蛇腹を通して固定しなければならない。よって,蛇腹のカメラ本体側の辺の長さは,余裕を見て縦42 mm,横37 mmとすればよいであろう。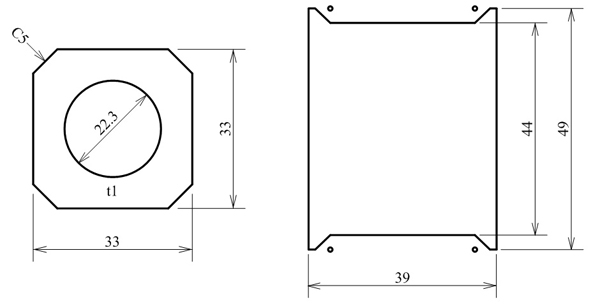
図2.レンズ取り付け座金(左)とカメラ本体側の切り抜き(右)の寸法
最後に③であるが,ベビースズカの蛇腹を伸張して測ったところ,43 mmであった。
以上で蛇腹を決定付ける最低限のデータは揃った。そこで仕上がり時の図を描くと図3のようになる。(寸法記号のAとBが前回の記事とは逆になっていることにご注意願いたい。)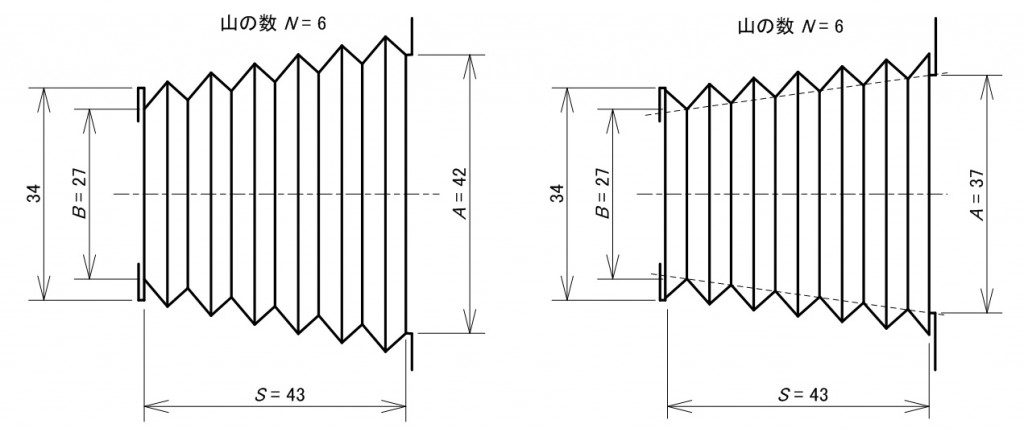
図3.蛇腹伸張時の寸法(左の図は側面,右の図は平面)
図3の両図でB=27とあるが,ベビースズカの蛇腹を計測したときそれぞれ27 mmおよび28 mmという値を得た。ただし,平面に関しては推測値である。両者は等しいはずであるから,測定値の信頼できる27 mmとした。
では蛇腹方程式に従って蛇腹の寸法を計算しよう。
表1をご覧いただきたい。これはExcelで計算した結果である。番号8に示したとおり,山の頂点の角度は90度とした。
計算式はすべて前回提示したものか,あるいは説明不要な一般的な事項である。ただし,番号17のhすなわち蛇腹を伸張したときの山の高さについては説明していなかった。これについては付録を参照願いたい。
行番号20のLsは両面で一致している。これは展開図を描くとき隣り合う2面がきっちり接続するということである。つまり,蛇腹全体の展開図が矛盾なく描けるということである。
さて,計算結果から山の斜面の長さは,側面についてはa=4.6680[mm], b=5.5014[mm]であり,平面についてはa=4.4810, b=5.7310[mm]が得られた。これらの数値と,A,BおよびLをもとに一つの面の展開図を描いた。図4をご覧いただきたい。
表1.蛇腹計算表(Baby Suzuka II用)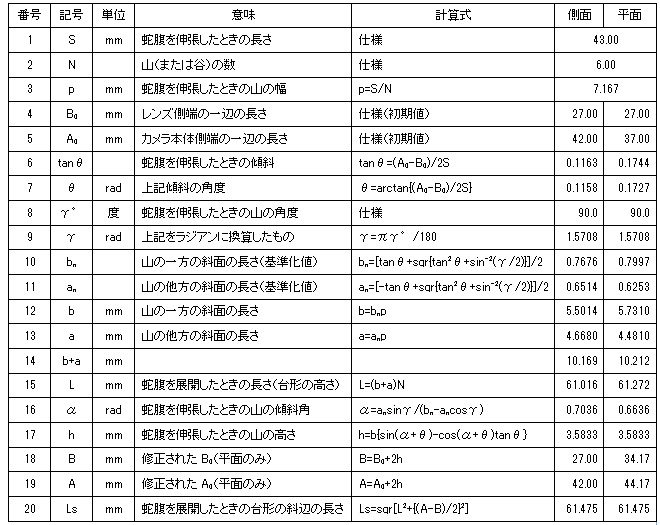
注.側面は山折りから,平面は谷折りから。
本格的なCADプログラムなどがあれば最初から完全な展開図が描けるのであるが,素人ではそうはいかない。そこで図4のような各面の展開図を描いて斜辺を一致させて4面つないでいく方法をとった。実際は貼り合わせるための「のりしろ」が必要なので5面描くことになる。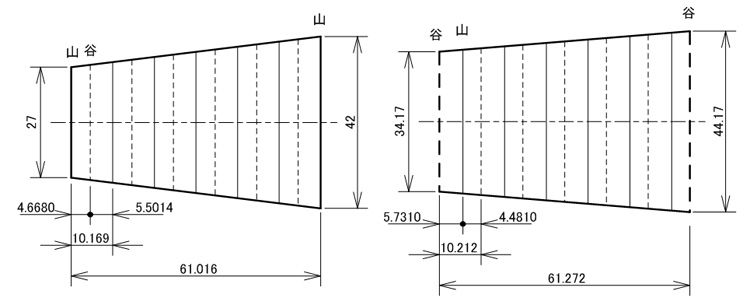
図4.蛇腹展開図の元になる台形図(左は側面,右は平面)
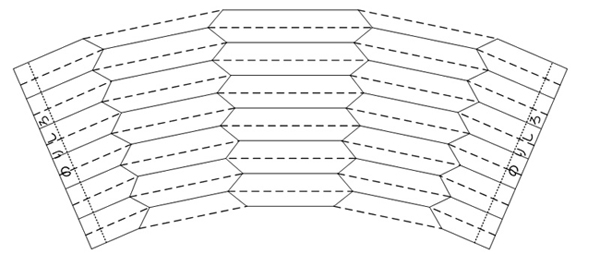
図5.蛇腹の展開図作図過程(実線は山折り,破線は谷折り)
亀吉は練習として三角定規,コンパス,デバイダなどを用いて作図したことがあるが,これは大変な作業であった。しかも出来栄えがよくない。さらに,ベビースズカの蛇腹は小さくて手作業による作図は困難である。
図5にジグザグの線があるが,これは隣り合う面の破線と実線との交点を結んだものである。(破線は図4に示したものから一部延長しなければならない。)
図6.蛇腹の展開図
後はこれをプリンタで印刷したものを線に沿って裁断し,のりしろ部分を接着して円錐台状の筒を作り,実線および破線に従って折り曲げればよい。
付 録
前回の記事「蛇腹方程式」での訂正や補足事項を以下に記す。
A1 訂正
式そのものが間違っているわけではないが,cosecは一般的ではないから使わないと言いながら使っていた。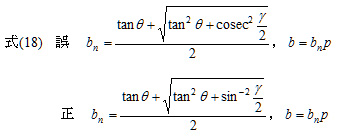
A2 修正
「2.1 台形の高さの計算」の箇所の説明が不適切であった。式(19)の2行後「一般に・・・」から始まる段落を以下のとおり改める。
一般にはNは正の整数と思われるが,0.5ほどの端数の付くことがある。これは山(または谷)から始まって谷(または山)で完結するような場合である。このような場合,台形の高さは![]()
または![]()
で計算できる。ここでNp はaとbのペアの数である。上記2つの式を式(19)で記述すればNが正の整数ではなくなるのである。式(19-1)を例にとれば![]()
となる。式(19)と比較すると![]()
という関係がある。a≒bであるから![]()
となる。これが「05ほどの端数が付く」と述べたことの意味である。つまり,端数の正確な値はa/(a+b)またはb/(a+b)である。
ただし,以上の議論は当然ながらaとbが決定された後でないと成り立たない。ところが,既に見たとおり,aとbを求めるためには蛇腹を伸張したときの傾斜tanθが必要である。そのtanθは図1のS,AおよびBが与えられれば求まる。図1は谷から始まって谷でおわっているが,山で終っていたらどうなるであろうか?tanθを求めるのに必要なBに相当する長さ(またはAに相当する長さ)がわからないのである。あるいはtanθを図4のpとqで求めようとしてもpがわからない。なぜなら,p=S/Nであるが,ここのNが(正確にはNの端数が)不明なのである。(ここでの端数はa/(a+b)またはb/(a+b)ではない。前回の記事では両者を混同していた。)
以上を要するに山の数Nが正の整数でないときは面倒になるということである。(前回の記事でp1やαを求めたが,これらはLを求めるためのNの端数に関する限り不要であった。)
A3 蛇腹を伸張したときの山の高さの計算
ここで問題の「山の高さ」を明確にしておこう。図A-1をご覧いただきたい。この図で頂点から垂線をおろし,斜辺と交差する点をMとする。このとき,頂点からMまでの長さhを山の高さとする。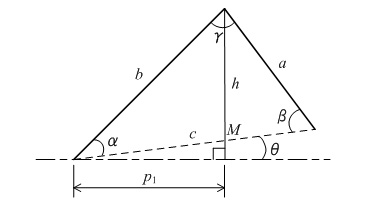
図A-1 山の高さを求める図
容易に
として求まる。
(次号に続く)
■2012年5月10日 木下亀吉
「わたしのカメラ三昧」に掲載されているすべての画像・文章は作者の木下亀吉様が所有しています、許可無く無断で複製・配布することはご遠慮下さい。